(a) Use um recurso gráfico para gerar o círculo e duas curvas de nível distintas de que somente toquem o círculo.
(b) Use os resultados obtidos na parte (a) para aproximar os valores máximo e mínimo de f sujeita à restrição .
(c) Verifique as suas aproximações da parte (b) usando multiplicadores de Lagrange.
Passo 1
Fala galera, vamos começar mais uma questão.
Letra (a) usando um recurso gráfico geramos esse gráfico para a questão.
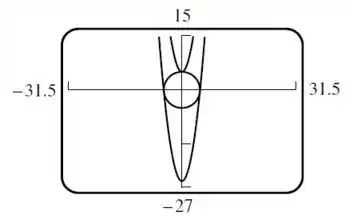
Passo 2
Agora vamos para a letra (b).
Usando o recurso gráfico temos que o valor mínimo é igual a . Já o valor máximo igual a .
Passo 3
Letra (c) Vamos aos cálculos usando os multiplicadores de Lagrange.
Fazendo as substituições em:
O que equivale a:
Substituindo em , temos:
Assim chegamos que o valor máximo é no ponto e valor mínimo é no ponto .
Acabamos essa, bora para a próxima?
Resposta
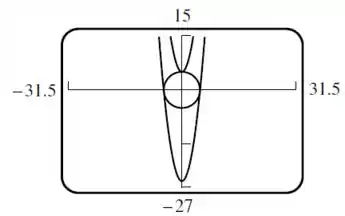
b) Valor mínimo . Valor máximo.
c) Valor máximo igual a no ponto e valor mínimo igual a no ponto .