(a) Use seu recurso gráfico para gerar a trajetória de uma partícula cujas equações do movimento no intervalo de tempo são
(b) Faça uma tabela das coordenadas e da partícula nos instantes .
(c) Em que instantes a partícula está sobre o eixo ?
(d) Durante qual intervalo de tempo temos ?
(e) Em que instante a coordenada da partícula atinge um máximo?
Passo 1
Fala pessoal, vamos fazer essa questão passo a passo.
Começamos com a letra (a), usando o Excel temos o seguinte gráfico para a trajetória da partícula.
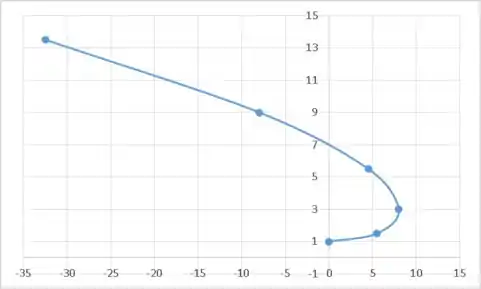
Passo 2
Letra (b) pede uma tabela com as coordenadas e da partícula nos instantes . Assim, temos:
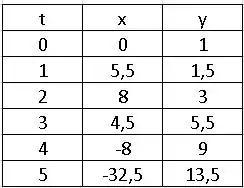
Passo 3
Letra (c) analisando o gráfico temos que a trajetória passa no eixo no ponto 1 e 7. Quando , temos que o . Para saber o quando faremos uma conta.
Assim temos que a partícula está sobre o eixo quando e .
Passo 4
A letra (d) pergunta durante qual intervalo de tempo temos . Vamos, inicialmente estipular em que instante fazendo a conta abaixo.
Agora, analisando o gráfico e a tabela, temos o intervalo de tempo onde encontramos é .
Passo 5
A letra (e) verificando o gráfico e a tabela, temos que a coordenada da partícula atinge um máximo no , após esse instante o valor de vai diminuindo, chegando a ser negativo.
Resposta
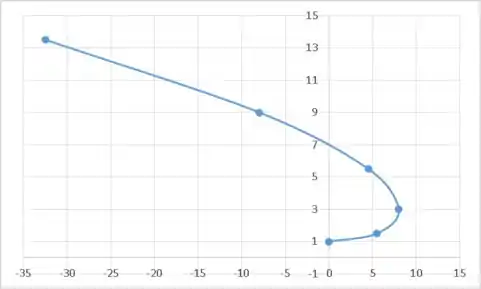
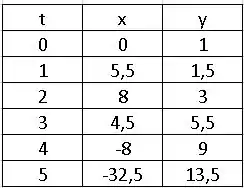
- e
- .