Use o teste da razão para a convergência absoluta (Teorema 9.6.5) para determinar se a série converge ou diverge. Se o teste for inconclusivo, aponte isso.
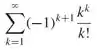
Passo 1
A primeira coisa para resolvermos essa questão é aplicar o teste da razão na equação geral, para isso colocaremos a equação geral da série no modelo:
Usando a série dada, temos os termos:
Passo 2
Logo:
Passo 3
Portanto,

Sabendo que então a série diverge.
Resposta
Diverge