Utilize triângulos semelhantes para encontrar as coordenadas do ponto Q que divide o segmento de P1(x1, y1, z1) a P2(x2, y2, z2) em dois comprimentos cuja razão seja p/q = r.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de vetores e a geometria do espaço.
Vamos agora resolver os exercícios da seção 2 sobre teoria e aplicações de vetores e geometria espacial.
Analisando o enunciado, podemos estabelecer o diagrama esquemático do que é pedido:
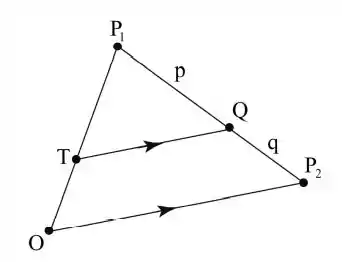
Sejam:
Escolhemos T em de modo que é paralelo a , assim tendo o triângulo TP1Q semelhante ao triângulo OP1P2. Então temos que:
Por semelhança:
Fazendo:
Teremos que:
Passo 2
Logo, as coordenadas do ponto Q são:
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.