Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 11.Problemas de Projetos - Ex. P7
Uma peça cilíndrica de aço com 75 mm (3 in) de diâmetro deve ser austenizada e temperada tal que uma dureza mínima de 40 HRC seja produzida em toda a peça. Dentre as ligas 8660, 8640, 8630 e 8620, qual irá se qualificar se o meio de têmpera for (a) água sob agitação moderada e (b) óleo sob agitação moderada? Justifique sua(s) escolha(s).
Passo 1
Pra resolver essa questão, vamos precisar interpretar dois gráficos que o capítulo 11 dá pra gente!
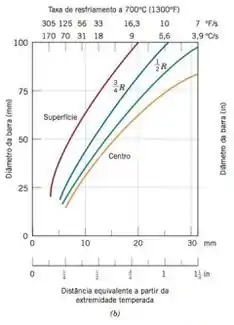
Esse primeiro descreve a taxa de resfriamento da têmpera em óleo em função do diâmetro em várias posições da peça.
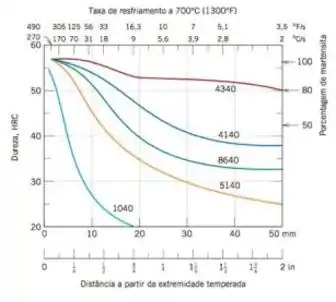
Esse segundo descreve a curva de temperabilidade pros 5 aços em questão.
Passo 2
Analisando os gráficos vemos que quase todos os aços atendem a exigência de dureza na superfície, exceto o 1040. No centro (à 12,5 mm de distância da superfície), apenas os aços 4140 e 4340 atendem as exigências.
Resposta
Apenas os aços 4140 e 4340 atendem todas as exigências.