29- Calcule o valor eficaz da forma de onda da corrente mostrada na Figura e a potência média liberada para um resistor de , quando a corrente percorre o resistor.
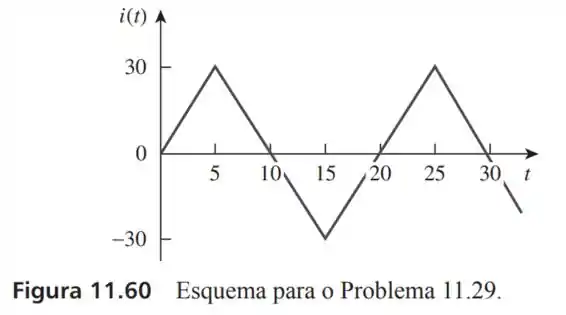
Passo 1
Para calcular a potência no resistor nós teremos que fazer:
E para calcular a corrente nós precisamos ver que essa onda tem um período de , além de redesenhar essa onda triangular da seguinte maneira.
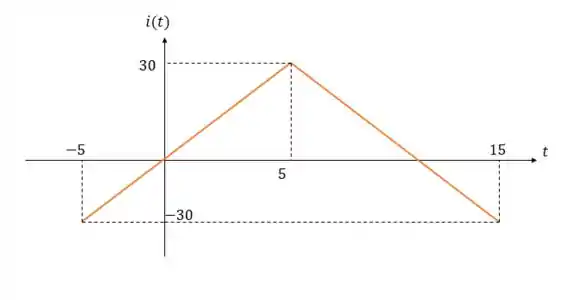
Figura para encontrar a equação da reta crescente.
E podemos calcular esse da seguinte forma:
Pois uma onda é o espelho da outra. E se colocarmos a origem do plano cartesiano onde está o tempo de nós encontramos essa segunda reta sem nenhuma perda de informação. (esse forma pode ser mais difícil de entender mas não precisa ficar descobrindo aonda a reta cruza com o eixo vertical e nem horizontal com o eixo de coordenadas estático como na figura acima.
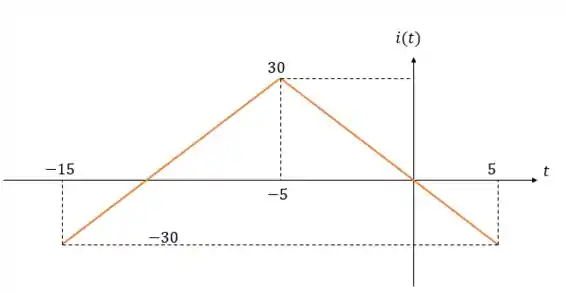
Figura para encontrar a equação da reta descendente
Logo:
Passo 2
Então a potência no resistor de será: