Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 78
78- Determine a leitura do wattímetro para o circuito mostrado na Figura
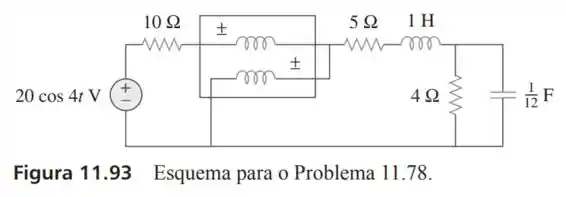
Passo 1
Os passos não serão diferentes da questão anterior pois a fonte continua sendo não e teremos que retirar a velocidade angular da fonte para calcular a reatância dos componentes passivos não resistivos.
Da fonte vemos que:
Então a reatância nos indutores e capacitores serão:
E o fasor da fonte não será:
Então nosso circuito ficará da seguinte maneira:
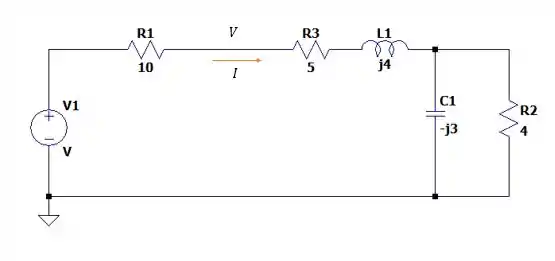
Onde precisamos encontrar a tensão naquela região e a corrente que passa por ali.
Passo 2
Para facilitar nossa vida vamos fazer a indutância equivalente entre a resistência de e a reatância de para encontrar :
Então a corrente será calculada por:
E a tensão naquela região será:
Passo 3
Então a potência complexa que passa pelo wattímetro será de (lembrando que a tensão e a corrente não estão em ):
Nos dando então uma potência real igual a: