Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 29
29. Utilizando a figura , elabore um problema para ajudar outros estudantes a entenderem melhor a análise de malhas.
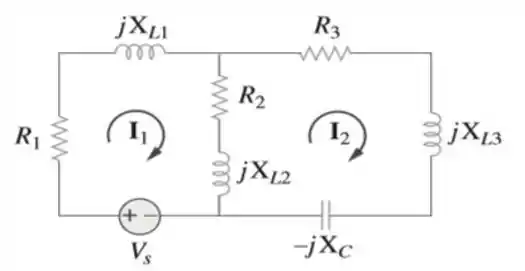
Passo 1
Fala galerinha! Vamos pra mais um problema sobre circuitos de corrente alternada .
Olha só! O nosso problema vai ser o seguinte. Iremos redesenhar esse circuito, atribuindo valores numéricos aleatórios aos componentes dele.
Bora lá! Mãos a obra!
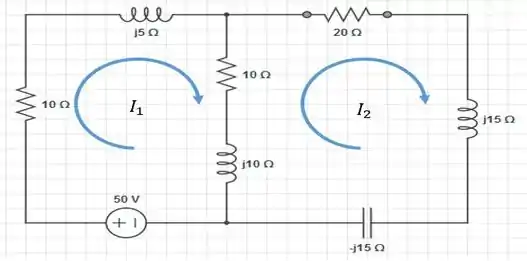
Passo 2
O nosso circuito já está completamente preparado pra análise de malhas.
Desse modo; aplicando a lei das tensões de para a malha , obtemos que:
E depois, fazendo a para a malha , chegamos à:
Passo 3
Então, precisamos resolver o sistema abaixo:
Passando para a forma matricial esse sistema...
Passo 4
A questão pede pra gente usar o !
Como não temos disponível, vamos usar um outro software bastante comum na graduação dos alunos de engenharia e que se assemelha muito ao . É o .
Olha só! O sistema do é fornecido através de três matrizes. Vamos dar nomes a elas:
A solução desse sistema, que é a matriz é dada no por:
Só que temos que adaptar essas matrizes à linguagem desse software.
A matriz fica assim:
E a matriz :
O reconhece o , que é a tradicional notação da forma fasorial, como . Sendo assim, colocando os dados no software, obtemos as seguinte respostas:
Essas são as nossas correntes de malha! Vamos escrever elas no domínio da frequência, seja lá qual for ela:
E pronto! Missão cumprida!