31. Use a análise de malhas para determinar a corrente no circuito da figura a seguir.
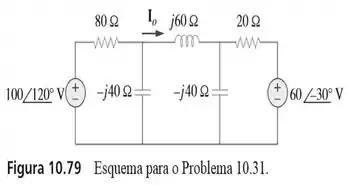
Passo 1
Fala galerinha! Vamos pra mais um problema sobre circuitos com corrente alternada.
Olha só! Todos os elementos do nosso circuito já estão na forma fasorial.
Bom pra gente, né não! Bora partir logo pra análise de malhas!
Passo 2
Agora, vamos preparar o circuito pra utilizar a nossa análise de malhas. Quando digo preparar, é simplesmente nomear as correntes de malha:

Desse modo... Aplicando a lei das tensões de para a malha , obtemos que:
E depois, fazendo a para a malha , chegamos à:
Por último, aplicamos a para a malha :
Passo 3
Então, precisamos resolver o sistema abaixo:
Que na forma matricial vai ficar igual à...
Passo 4
A questão pede pra gente usar o !
Como não temos disponível, vamos usar um outro software bastante comum na graduação dos alunos de engenharia e que se assemelha muito ao . É o .
Olha só! O sistema do é fornecido através de três matrizes. Vamos dar nomes a elas:
A solução desse sistema, que é a matriz é dada no pelo produto da inversa da matriz pela matriz :
Só que temos que adaptar essas matrizes à linguagem desse software.
A matriz fica assim:
E a matriz :
O reconhece o , que é a tradicional notação da forma retangular, como . Sendo assim, colocando os dados no software, obtemos as seguinte respostas:

Essas são as nossas correntes de malha!
Agora bora dar uma olhada na figura do . Repara que a corrente de malha , é extamente a corrente do enunciado.
Sendo assim...
E pronto! Vamos deixar no domínio da frequência mesmo! Missão cumprida!