Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 49
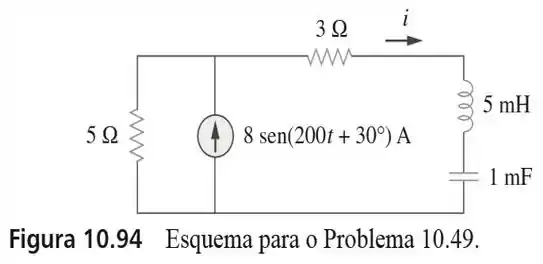
49. Usando a transformação de fontes, determine no circuito da figura .
Passo 1
Fala galerinha! Bora pro nosso primeiro probleminha sobre transformação de fontes.
Olha só! A parte do circuito que contém uma resistência de e uma corrente de em paralelo; pode ser transformada em uma associação em série entre a mesma resistência e uma fonte de tensão, que é dada por:
Passo 2
Depois, bora passar os elementos pro domínio da frequência:
E o nosso circuito fica do seguinte jeito:
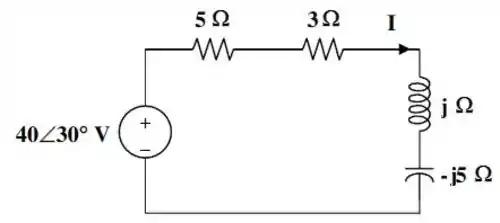
E a corrente vai ser dada pela divisão da fonte de tensão pela impedância total do circuito
Passando pro domínio do tempo:
Pronto! Resposta obtida!
Resposta
Exercícios de Livros Relacionados
51. Use a transformação de fontes para determinar I 0 no circuito do problema 10.42
O PSpice é capaz de tratar um circuito com duas fontes independentes de frequências diferente. Verdadeirob) falso
Consulte o circuito da Figura 10.49. A impedância equivalente de Norton nos terminais a-b é: - j 4Ω b) - j 2Ω c) j 2Ω d) j 4Ω
Consulte o circuito da Figura 10.49. A impedância equivalente de Norton nos terminais a-b é: - j 4Ω b) - j 2Ω c) j 2Ω d) j 4Ω
Consulte o circuito da Figura 10.47 e observe que as duas fontes não têm a mesma frequência. A corrente i x t pode ser obtida por:Transformação de fontesTeorema da superposiçãoPSpice