Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 54
54. Refaça o problema usando a transformação de fontes
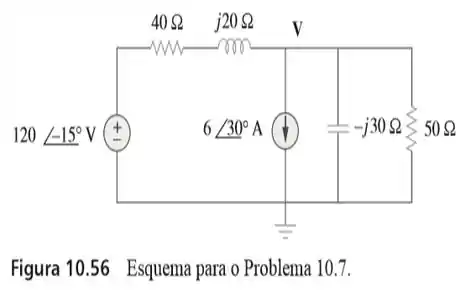
Passo 1
A primeira coisa que temos que fazer é pensar num jeito de tornar esse circuito mais fácil pra gente trabalhar.
Por isso, vamos usar a transformação de fontes nessa parte aqui do circuito destacada de preto...
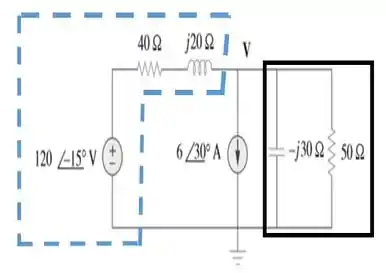
Bora calcular a impedância equivalente, para a parte do circuito envolta pelo retângulo preto. Ela é dada por:
Multiplicando essa impedância pela fonte de corrente de , obtemos o valor da tensão representada pela associação em paralelo entre a impedância e a fonte de corrente.
Passo 2
Na prática,o que fizemos foi usar novamente uma transformação de fonte. De uma associação em paralelo entre uma fonte de corrente e uma impedância, ficaremos com uma associação em série entre uma fonte de tensão e a mesma impedância.
Desse jeito aqui:
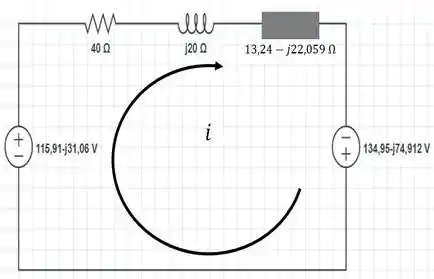
Em seguida, usando o , bora determinar o valor da corrente nesse nosso circuito modificado, de apenas uma malha:
E a tensão , que é o que nós queremos obter, temos que é dada por:
Passando para a forma polar:
Resposta
E pronto! Resposta Obtida!