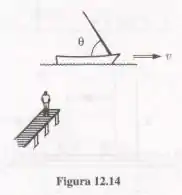
Um barco foi fabricado de modo que o mastro se incline em um ângulo em relação ao convés. Um observador em pé no cais vê o barco passar em velocidade v (Fig. 12.14). Que ângulo esse observador diz que o mastro está?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Vamos considerar o para ser o comprimento do mastro inclinado em ângulo .
A componente x do comprimento do mastro será de e a componente y do comprimento do mastro é .
O movimento do barco é ao longo da direção x, portanto, a contração do comprimento será observada apenas ao longo da direção x, enquanto o componente y do comprimento permanece inalterado.
A componente vertical do comprimento observada pelo observador é .
O componente de comprimento horizontal do mastro é contraído a um comprimento de
é o comprimento contraído ,
Passo 2
O ângulo observado por um observador no cais é
Passo 3
Como sabemos quem é gamma iremos substituir ele
Portanto, o ângulo observado por um observador no cais é de
Resposta
Portanto, o ângulo observado por um observador no cais é de