Um brinquedo conhecido consiste de ímãs permanentes em forma de rosquinha (magnetização paralela ao eixo), que deslizam sem atrito em uma haste vertical (Figura 6.31). Trate os ímãs como dipolos, com massa e momento de dipolo m.
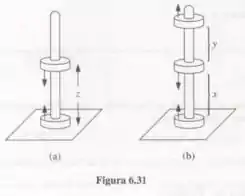
- Se você colocar os ímãs na haste com os lados correspondentes voltados um para o outro, o ímã de cima “flutuará” - a força magnética para cima anulará a força gravitacional para baixo. A que altura (𝑧) ele flutua?
- Se você acrescenta um terceiro ímã (paralelo ao de baixo), qual será a razão entre as duas alturas? (Determine o valor de fato com três algarismos significativos)
Passo 1
Olá, pessoal. Bora para mais uma!?
Antes de iniciar a solução da questão vamos introduzir a equação 5.86 representadas abaixo:
Como no nosso caso e é na direção z sendo que , temos que:
Associando a parte de baixo do brinquedo, temos que:
Agora que temos a relação para o campo magnético, podemos associar com a força magnética pela equação 6.3, assim temos que:
Para que o imã de cima flutue , sendo que P é o peso do imã. Assim temos:
Com isso podemos saber a altura que ele ficara suspenso.
Passo 2
Agora temos um imã colocado acima paralelo aos outros dois. A força magnética que o ímã de cima realiza no do meio é análoga a força calculada no item (A), sendo assim temos
Vale ressaltar que foi escrito pois é a distância associada.
Sendo assim. Para saber a distância x e y mostrada na figura, temos que:
Sendo que , e , com isso, temos que:
Essa expressão representa as forças sobre o ímã do topo.
Agora vamos escrever as equações para o ímã do meio:
Com isso temos que:
Subtraindo a expressão do imã meio da do de cima e resolvemos para desaparecer tudo aquilo que não é interessante, temos que:
Agora vamos multiplicar os parênteses por (-1):
Perceba que podemos anular os termos (:
Colocando em evidência:
Podemos dividir tudo por
Somamos dos dois lados da equação e multiplicamos tudo por
Vamos definir , com isso temos que
Com isso conseguimos encontrar o valor de 0.850114979537622
E assim finalizamos mais uma questão, te espero na próxima.
Resposta
- 0.850114979537622