Um cabo coaxial longo (Figura 2.26) possui uma densidade volumétrica de carga uniforme no cilindro interno (raio ), e uma densidade superficial de carga uniforme na casca externa do cilindro (raio ). Essa carga superficial é negativa e de magnitude exata para que o cabo, como um todo, seja eletricamente neutro. Encontre o campo elétrico em cada uma das regiões: (i) dentro do cilindro interno (), (ii) entre os dois cilindros (), (iii) externa ao cabo (). Faça um gráfico de como função de .
Passo 1
Falaaa, tudo belezaa?? Para acharmos o campo elétrico com a lei de Gauss usamos a fórmula abaixo:
Quer dizer que a integral do campo elétrico em uma superfície fechada é igual a carga envolvida dividida por uma constante. O que precisamos agora é definir a superfície e a carga envolvida. Bora lá!!!
Passo 2
A imagem do cabo pode ser analisada abaixo:
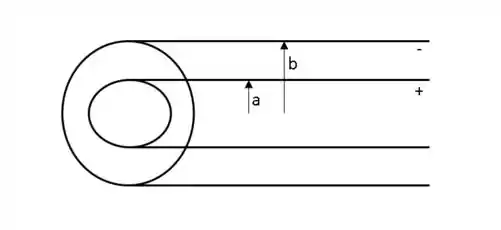
Podemos considerar as duas partes do cabo como dois cilindros, um de raio e outro . Portanto, no caso de , o raio do cilindro da superfície Gaussiana é menor que o cilindro positivo.
Os dois cilindros têm densidade de carga uniforme, então a carga envolvida é:
E a superfície de Gauss é a superfície de um cilindro. Substituindo na lei de Gauss.
Passo 3
Quando o raio da superfície de Gauss for maior que e menor que . Estaremos considerando todo o cilindro menor. E a carga envolvida agora depende do volume do cilindro menor do cabo.
E a superfície de Gauss continua sendo a mesma.
Passo 4
O enunciado nos diz que o cabo está disposto de um modo que a carga total externa é zero, pois, a casca externa do cabo é negativa. Então, o campo elétrico quando a superfície Gaussiana é maior que o cabo é zero.
Passo 5
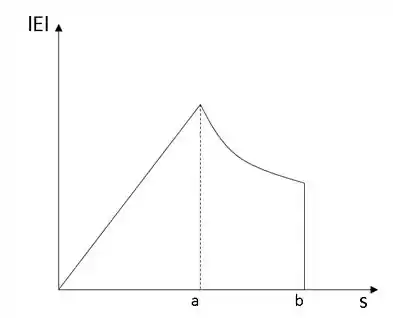
O gráfico de em função de pode ser analisado abaixo: