- Calcule cada uma das seguintes funções e verifique se ela é periódica. Se for periódica, determine seu período.
Passo 1
Qualquer função periódica pelo teorema de Fourier pode ser expressa por:
E para ela ser periódica de fato as funções que compões a precisam ter o mesmo e por consequência o mesmo além de ter uma relação entre os .
Então por exemplo a letra nos diz que:
E podemos dizer que existe com , e estaríamos aproveitando somente os harmônicos ímpares, ou seja o que nos leva a um período igual a:
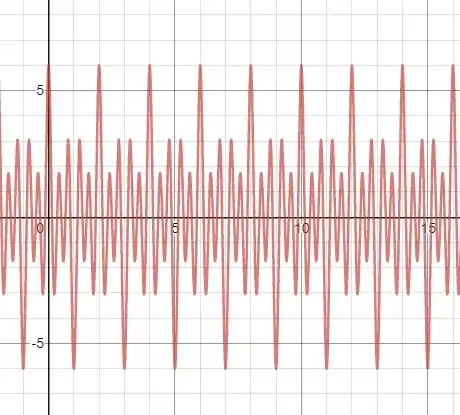
Então a letra é sim períodica.
Com gráfico:
Passo 2
Já na letra não conseguimos estipular um valor de pois na função seno ele vale :
E na função cosseno ele pode valer:
Com
Então por duas ondas terem períodos diferentes não é possível traçar um período só para a onda toda, para esse tipo de onda nós chamamos ela de batimento então ela não pode ser representada por Fourier.
E a primeira coisa que todas as funções trigonométricas tem que ter são os mesmos valores de . Então a função não é periódica mesmo as duas funções (seno e cosseno) serem periódicas.
Isso ficará mais claro pelo gráfico da letra .
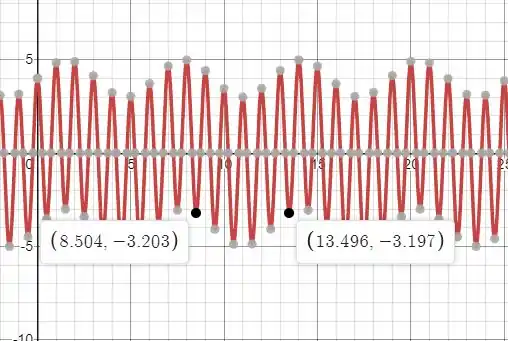
Essa função tem toda a cara de ser periódica, mas acredite tem pequenas diferenças entre alguns valores de pico e vale. Isso se deve ao fato de termos uma função composta por outras duas funções que são períódicas, mas com levemente diferentes.
Passo 3
Agora a letra pode ser escrita da seguinte forma:
Então:
Só que como então:
Como temos a mesma função seno então podemos dizer que:
Nos dando o seguinte gráfico
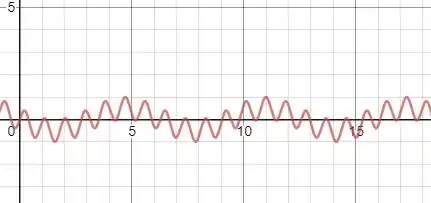
Sendo sim uma função periódica. Uma vez que podemos escrever as duas funções com o mesmo e valores diferentes de .
Passo 4
Já a letra pode ser escrita como:
Supondo vemos que a função tem logo, , nos dando o seguinte gráfico.
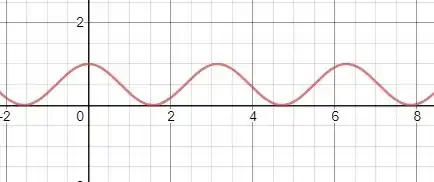
Portanto a função é sim periódica.
Passo 5
Na letra temos a forma alternativa da série de Fourier que é a forma amplitude-fase que é escrita na seguinte forma:
E podemos escrever a função da seguinte forma:
Sim, eu sei não é trivial escrever a série dessa forma, mas note que temos duas funções com e uma vale:
E como as duas estão na mesma função seno, podemos forças dizendo que na primeira e na segunda . Então um jeito de fazer com que nos dois seja igual é fazendo:
Com
Então , logo:
Sendo sim uma função periódica.
Passo 6
A letra pode gerar uma discussão filosófica interessante, pois independente do período que você escolha, a função constante terá um comportamento conhecido, sempre começando e terminando no mesmo valor.
Isso é supondo que o período da reta é de , nós temos que:
Nesse sentido a função constante pode ser vista como periódica, mesmo ela não variando nada, meio louco isso mas é a definição para uma função ser periódica.
No caso de Fourier é como se tivéssemos:
E a letra é uma função exponencial e que não tem nenhuma relação com a série de Fourier exponencial e complexa.