Calcule a integral de volume da função para o tetraedro com cantos em , , e .
Passo 1
Fala galera! Lembrando como calculamos a integral de volume:
Passo 2
Com os pontos dados, teremos o seguinte tetraedro:
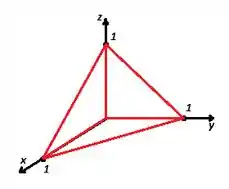
Podemos ver que seus termos se relacionam da seguinte forma:
Logo, podemos definir a variação dos termos da seguinte forma:
Assim, nossa integral ficará:
Resposta
Então, a integral de volume da função para p tetraedro dado vale
Qualquer dúvida, pode mandar pra gente!