Uma carga q é liberada do repouso na origem, na presença de um campo elétrico uniforme de um campo magnético uniforme . Determine a trajetória da partícula transformando para um sistema no qual , encontrando o caminho nesse sistema e depois transformando de volta para o sistema original. Assuma que . Compare o seu resultado com o exemplo 5.2.
Passo 1
Faaaaaala, galera... Tranquileba??
Transformando o sistema para um sistema pedido:
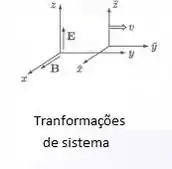
E reescrevendo aa equação 12.108
E:
E como dito:
De modo que:
Se queremos que
E para
Dado
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para a trajetória em desde que a partícula começou em repouso na origem em S, ela começou com velocidade em
Temos na equação 12.72 que:
O que demonstra que a partícula percorre em circulo
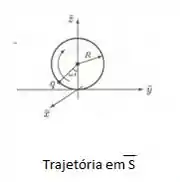
Assim a trajétoria então é:
Para a trajetória em , pela transformação de Lorentz da eq. 12.18 e 12.19 temos:
E do outro lado:
Assim:
Passo 3
Assim podemos fazer o seguinte sistema:
Assim obtemos: