Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 36

A chave do circuito mostrado na Figura P7.36 esteve na posição a por um longo tempo antes de passar para a posição b em t = 0. a) Determine as expressões numéricas para i L(t) e vo (t) quando t $ 0. b) Determine os valores numéricos para vL(0+) e vo (0+).

Passo 1

[a] - Para t < 0 : o indutor se comporta um curto circuito depois de um longo tempo no mesmo estado, então o circuito se reduz a esta configuração:

i L 0 - = 32 20 = 1,6   A

Para t > 0 , a chave muda de posição, logo a configuração do circuito também muda, ficando desse jeito aqui:

i L ∞ = 32 - 48 12 + 8 = - 0,8   A

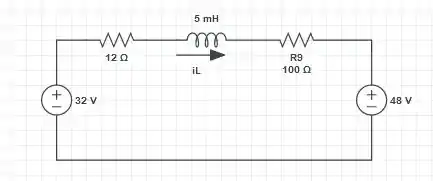
Calculando a constante de tempo:

τ = L e q R e q = 5 × 10 - 3 12 + 8 = 250   μ s → 1 τ = 4000

Agora, usando a equação geral, podemos encontrar a equação da corrente:

i L = i L ∞ + i L 0 + - i L ∞ e - t / τ  

Substituindo os valores numéricos, temos:

i L =   - 0,8 + 1,6 + 0,8 e - 4000 t =   - 0,8 + 2,4 e - 4000 t   A ,     t ≥ 0

O v 0 é o somatório da tensão no resistor de 8   Ω com a fonte de tensão de 48 V, logo:

v 0 = 8 i L + 48 = 8 - 0,8 + 2,4 e - 4000 t + 48

v 0 = 41,6 + 19,2 e - 4000 t   V ,     t ≥ 0 +

Passo 2

[b] – Para encontrar a tensão no indutor, é basicamente usar a fórmula v L = L d i L d t , então:

v L = L d i L d t = 5 × 10 - 3 - 4000 2,4 e - 4000 t

v L = - 48 e - 4000 t   V ,     t ≥ 0 +

Sendo o v L 0 + =   - 48   V e v 0 0 + = 0   V

Resposta

a )   i L t = - 0,8 + 2,4 e - 4000 t   A ,     t ≥ 0

v 0 = 41,6 + 19,2 e - 4000 t   V ,     t ≥ 0 +

b )   v L 0 + =   - 48   V   e   v 0 0 + = 0   V

Exercícios de Livros Relacionados

A constante de tempo para um circuito R L com R = 2 Ω e L = 4 H é:(a) 0,5 s (b) 2 s (c) 4 s (d) 8 s (e) 15 s
Para o circuito da figura 7.91, determine i_0 para t = 0 .
Usando a figura 7.92, elabora um problema para ajudar outros estudantes a entenderem melhor os circuitos R L sem fonte.
Usando a Figura 7.118, elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito R L .
Em vez de aplicar a técnica reduzida usada na Seção 7.6, use a LKT para obter a Equação (7.60).