Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 24
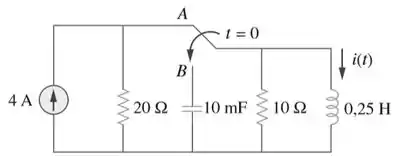
A chave da Figura 8.77 muda da posição A para a posição B em t = 0 (observe atentamente que a chave tem de se conectar ao ponto B antes de ela desfazer a conexão em A, um interruptor). Determine para .
Passo 1
Relaxa, galera. Vamo se Ligar e achar a Resposta. Questão bem tranquila pessoal! Quando o interruptor está na posição A, o indutor age como um curto circuito!
Quando o interruptor está na posição B, temos um circuito em pararelo, logo:
Passo 2
Como o , temos um caso de subamortecimento!
Resposta
Exercícios de Livros Relacionados
Usando a Figura 8.78, elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos R L C sem fontes.
Dado o circuito sem fne da Figura 8.114 , use o PSpice ou o MultiSim para obter i ( t ) para 0t20s . Suponha v 0 = 30V e i 0 = 2A .
Elabora um problema, para ser resolvido usando o PSpice ou o MultiSim, de forma a ajudar outros estudantes a entenderem melhor os circuitos R L C sem fonte.
O circuito da Figura 8.123 é um modelo elétrico das funções corpóreas usadas em faculdades de medicina para estudo de convulsões. Esse modelo tem as seguintes características: C 1 = Volume de fluido e
Um oscilograma pode ser modelado de forma adequada por meio de um circuito de segunda ordem na forma de um circuito R L C em paralelo. Deseja-se obter uma tensão subamortecida no resistor de 200Ω . Se