Um cilindro infinitamente longo de raio R, tem magnetização ‘congelada’ paralela ao eixo,
Onde é uma constate e é a distância ao eixo. Não há corrente livre em lugar algum. Encontre o campo magnético dentro e fora do cilindro por dois métodos diferentes:
a) Como na seção 6.2, localize todas as correntes ligadas e calcule o campo que elas produzem.
b) Use a lei de Ampère (na forma da equação 6.20) para encontrar H, e em seguida obtenha B a partir da Equação 6.18. (Observe que o segundo método é muito mais rápido e evita qualquer referência explicita às correntes ligadas)
Passo 1
Olá pessoal, essa é uma questão para testar métodos. Para ficar mais clara a análise, vamos representar um pequeno pedação do fio.
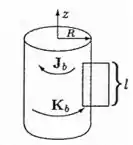
a) Neste caso, teremos a magnetização escrita como:
As correntes superficiais e volumétricas aqui, serão representadas por:
E
B está na direção z (esta é essencialmente uma superposição de solenoides).
Então do lado de fora. Para o campo na parte de dentro, vamos utilizar a linha amperiana desenhada na figura, onde:
Onde I é escrito por:
Assim, podemos escrever I como:
Retornando a equação do campo, temos:
Então o campo no interior do fio será:
Passo 2
b) Por simetria, H aponta na direção z. Essa mesma linha amperiana fornece:
pois não há correntes livres aqui. Então H = 0 e, portanto:
- Dentro, temos:
- E fora, temos:
- Dentro, temos:
- E fora, temos:
Resposta
As considerações e desenvolvimento do segundo métodos realmente tornou as coisas mais simples e ágeis, nos fazendo chegar a um mesmo resultados, onde:
Resposta
Ei, a resposta está no passo a passo :)