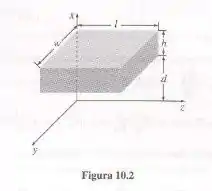
Para a configuração no Exemplo 10.1, considere uma caixa retangular de comprimento , largura e altura , situada a uma distância acima do plano (Figura 10.2).
a) Encontre a energia na caixa no tempo e em .
b) Encontre o vetor de Poynting e determine a energia por unidade de tempo que flui para dentro da caixa no intervalo .
c) Integre o resultado em (b) de a e confirme que o aumento de energia (parte (a)) é igual a ao influxo líquido.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Os campos elétrico e magnético para são:
No instante , a ativação da corrente acaba de chegar ao fundo da caixa e, portanto, não há energia nela. No instante a 'onda' atingiu o topo da caixa e a densidade de energia na caixa é:
Desenvolvendo um pouco mais
Com isso, nós temos que
Onde nós utilizamos . A energia total é dada por
Que será igual a
Passo 2
B – O vetor de Poynting é dado por:
Substituindo os valores, nós temos que
Com isso, nós temos que
Com isso, nós temos que
Substituindo novamente
Já que estamos interessados no fluxo de energia no plano .
Passo 3
C - A energia total que entra na caixa pela parte inferior é, portanto, a integral do tempo dos tempos a :
Que nos dá o seguinte resultado
Que é o mesmo que a) parte do problema, como deve ser.