Uma demonstração conhecida de supercondutividade é a elevação de um magneto sobre um pedaço de material supercondutor. Esse fenômeno pode ser analisado usando-se o método das imagens. Trate o magneto como um dipolo perfeito m, a uma altura acima da origem (e restrito a apontar na direção ), e faça de conta que o supercondutor ocupa todo o semi-espaço abaixo do plano Devido ao efeito meissner, para , e como tem divergente nulo, o componente normal é contínuo, de forma que logo acima da superfície. Esta condição de contorno do contorno é satisfeita pela configuração de imagem na qual um dipolo idêntico é colocado em , como substituto do supercondutor, os dois arranjos, portanto, produzem o mesmo campo magnético na região
a) em que sentido o dipolo da imagem deve apontar
b) encontre a força no magneto devido às correntes induzidas no supercondutor (o que equivale a dizer a força devida ao dipolo da imagem). Considere-a igual a Mg (onde M é a massa do magneto) para determinar a altura h na qual o magneto irá flutuar.
c) a corrente induzida na superfície do supercondutor pode ser determinada a partir da condição de contorno ao componente tangencial. Usando o campo que você obtém a partir da configuração de imagem mostre que:
onde é a distância à origem.
Passo 1
Fala aiii meus lindos tudo blz? espero que sim
Então se liga só nessa questão do livro David J. Griffiths de Eletrodinâmica uma demonstração conhecida de supercondutividade é a elevação de um magneto sobre um pedaço de material supercondutor. Esse fenômeno pode ser analisado usando-se o método das imagens. Trate o magneto como um dipolo perfeito m, a uma altura acima da origem (e restrito a apontar na direção ), e faça de conta que o supercondutor ocupa todo o semi-espaço abaixo do plano Devido ao efeito meissner, para , e como tem divergente nulo, o componente normal é contínuo, de forma que logo acima da superfície. Esta condição de contorno do contorno é satisfeita pela configuração de imagem na qual um dipolo idêntico é colocado em , como substituto do supercondutor, os dois arranjos, portanto, produzem o mesmo campo magnético na região
a) em que sentido o dipolo da imagem deve apontar
b) encontre a força no magneto devido às correntes induzidas no supercondutor (o que equivale a dizer a força devida ao dipolo da imagem). Considere-a igual a Mg (onde M é a massa do magneto) para determinar a altura h na qual o magneto irá flutuar.
c) a corrente induzida na superfície do supercondutor pode ser determinada a partir da condição de contorno ao componente tangencial. Usando o campo que você obtém a partir da configuração de imagem mostre que:
onde é a distância à origem.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Na letra (a) para tornar o campo paralelo ao plano, precisamos de monopolos de imagem com mesmo sinal temos como representação,
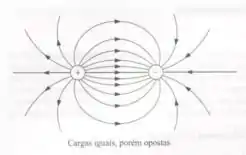
Com isso a imagem aponta para
Na letra (b) para temos,
Logo,
e por fim na letra ( c ) para determinar a distância da origem temos,
Mas,
Logo,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)
c)