Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 47
Determine para o circuito na Figura .
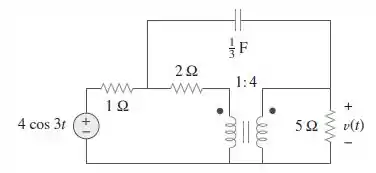
Passo 1
Primeiramente, vamos transformar os elementos do circuito que estão no domínio do tempo para o domínio da frequência:
Aplicando a lei das malhas na malha da esquerda:
Aplicando a lei das malhas na malha do meio:
Similarmente, aplicando a lei das malhas na malha da direita:
Nos terminais do transformador, temos:
Passo 2
Aqui, caímos num sistema de equações, com cinco equações e cinco incógnitas:
Escrevendo de modo matricial:
Uma maneira de encontrarmos os valores para as incógnitas é usar a regra de Cramer! Primeiro de tudo, precisamos achar o determinante da matriz:
Agora, vamos calcular os determinantes substituindo o vetor nas colunas de cada variável. Assim, para :
Para
Para
Para :
Para
Passo 3
Para encontrarmos os valores de cada uma das variáveis, precisamos dividir o determinante de cada uma pelo determinante da matriz . Logo,
Como está em paralelo a ,
Passando para o domínio do tempo,
Resposta
A tensão é igual a: