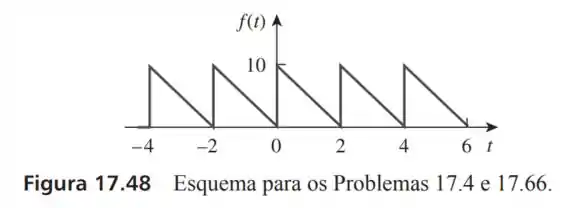
4- Determine a expansão em série de Fourier da forma de onda mostrada na Figura . Determine os espectros de amplitudes e de fases.
Passo 1
O período dessa onda é de:
Dessa forma será:
E o comportamento dessa onda no período de até é:
Pois quando , e quando ,
Passo 2
Dessa forma vamos calcular os parâmetros da série de Fourier:
Passo 3
Agora será:
Então:
Onde:
Uma vez que é um número inteiro.
Então:
Fazendo integração por partes temos:
Onde:
Então:
Aplicando esse intervalo vemos que:
Assim como para inteiro e :
Então:
Passo 4
Agora para o valor de temos:
Isso será:
Isso será:
Onde:
Pois sempre será inteiro.
Então:
Fazendo integração por partes temos:
Onde:
Então:
Já que é um número inteiro, então:
Dessa forma:
Passo 5
Com esses coeficientes nós temos:
E plotando 100 pontos nós teremos o seguinte gráfico.
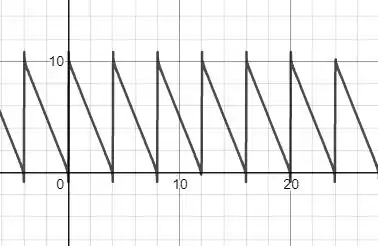
E isso nos diz que estamos certos...
Passo 6
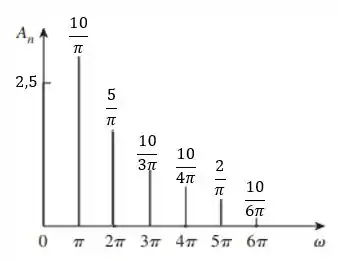
Para os espectros de amplitude e de fase, temos que fazer os gráficos de () e com .
Primeiro, plotando com :
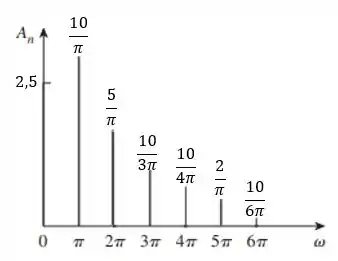
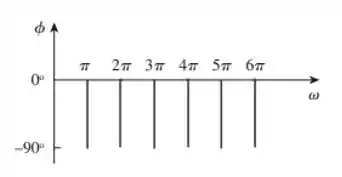
Agora, fazendo o espectro de fase:
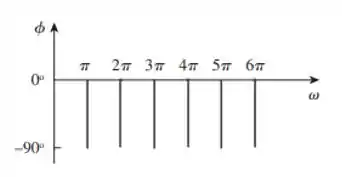
Beleza?? Fechamos o exercício! 😊
Resposta