Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 22
Determine a função de transferência de Bode de magnitude mostrado na figura.
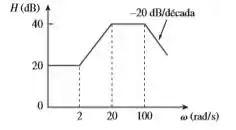
Passo 1
Para resolver esse problema, vamos nos basear nessa tabela aqui:
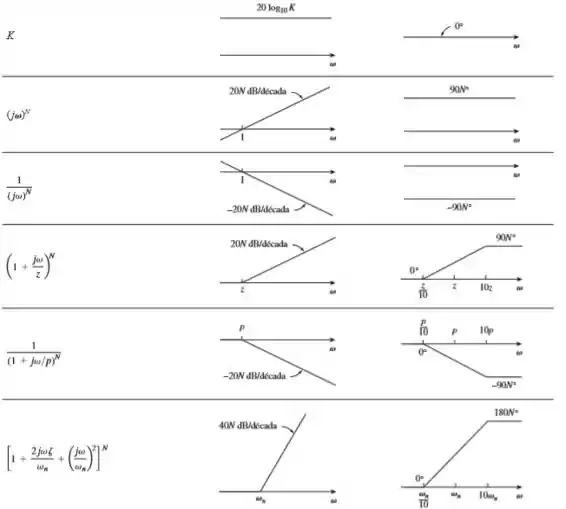
Vamos nessa?
Passo 2
A parte reta em que vai até é devido o ganho . Para a gente encontrar o valor desse cara a gente tem que igualar...
Saca?
Passo 3
Em a gente tem um zero de , o que corresponde a linha da nossa tabela:
Passo 4
De até , a gente tem uma constante em . Ora bolas, a gente acabou de ver que tínhamos uma reta crescente de antes de Para formar uma constante, a gente tem que subtrair a partir de . Em forma de desenho...
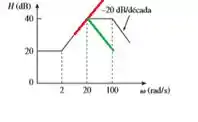
Onde a reta vermelha é devido ao zero do passo 3 e a reta verde corresponde a um polo de em (linha da nossa tabela):
Passo 5
De em diante a gente tem mais um decaimento de . O que significa novamente que temos um polo em ...
Passo 6
Juntando tudo então, a gente conclui que é o produto de todo mundo...
Multiplicando em cima e em baixo por ...
Então...
A gente pode trocar por ...