Determine a impedância equivalente do circuito da Figura 9.80.
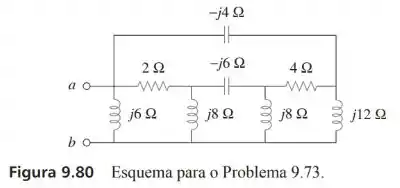
Passo 1
Podemos perceber a presença de várias associações do tipo que nomearemos para cada nó do meio de e esses valores são obtidos fazendo
Agora temos para o resto do circuito
Como temos 2 associações do tipo coladas uma na outra vamos ter mais pontos importantes e que serão calculados com base no resultado de , assim, temos
Calma que já estamos acabando, resta-nos, calcular algumas impedâncias que estão em paralelo para termos todo o aparato necessário para encontrarmos a impedância equivalente total do nosso circuito. Então, tomemos as seguintes associações em paralelo
Passo 2
Pronto, agora temos tudo o que precisamos para calcular a impedância equivalente total do nosso circuito basta fazermos