Dois fios longos e retos com densidades lineares uniformes e opostas estão situados em cada um dos lados de um longo cilindro condutor (Figura 3.39). O cilindro (que não tem carga líquida) tem raio , e os fios estão a uma distância a do eixo. Encontre o potencial no ponto .
Passo 1
Falaa galera, bora iniciar mais uma questãozinha do nosso livro!
Essa questão é um pouquinho trabalhosa, mas vem comigo pra gente fazer passo a passo!
De acordo com a Figura 3.39, temos:
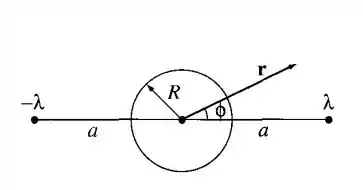
Fazendo:
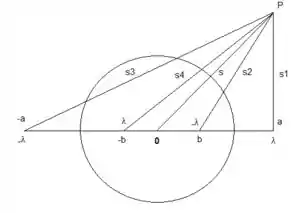
Pela a imagem acima, colocando as cargas nas linhas da imagem em . O potencial de uma carga de linha é:
Onde é a distância da linha. Somando agora os potenciais de todos os fios, temos:
Assim:
Tudo certinho? Vamos pro próximo passo!
Passo 2
Agora a gente precisa que a expressão anterior sob o logaritmo seja constante para , assim:
Isso será constante para todo se colocarmos , desde então:
Depois de multiplicar o numerador e o denominador por . Se colocarmos as cargas de linha da imagem em a superfície será equipotencial e não importará o valor de .
Dessa forma, o potencial total é apenas 1 com :
E com isso a gente conclui nossa questãozinha, te vejo na próxima!