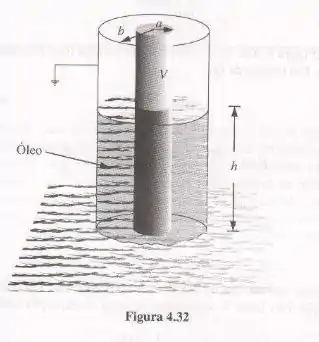
Dois tubos longos de metal, cilíndricos e coaxiais (raio interno a, raio externo b) estão colocados verticalmente em um tanque de óleo (suscetibilidade , densidade de massa ). O tubo interno é mantido a um potencial , enquanto o externo está aterrado (Figura 4.32). A que altura o óleo sobe no espaço entre os tubos?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Vamos lá, para fazer uso da equação 4.67 , nós precisamos encontrar a capacitância como uma função da altura , ok? Vamos chamar nesse caso de . Considerando a altura total do cilindro como , deixando as cargas das linhas como para o ar e para o caso do óleo. Os campos elétricos que serão associados a essas diferenças de potencial são respectivamente,
Com isso, nós teremos que a ddp é
Para o caso do óleo,
Com isso, a ddp é igual a
As diferenças de potencial tem que ser as mesmas para o ar e para óleo, então
Com isso, a carga total do cilindro é igual a
Desenvolvendo um pouco mais os termos, nós temos que
Em termos de susceptibilidade, podemos escrever essa equação da seguinte forma
Passo 2
Tendo tudo isso em mente, podemos encontrar a capacitância, dada a seguinte fórmula
Nós temos o e o (de forma indireta), então tendo em mente a substituição
Percebeu que agora nós já podemos encontrar a equação 4.67, então utilizando a mesma
Finalmente, do equilíbrio desta força (para cima) e da força gravitacional (para baixo), obtemos a altura do fluido
Isolando o , logo
E encontramos a altura! 😊