Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 6

As duas chaves no circuito visto na Figura P7.6 são sincronizadas. Elas estiveram fechadas por um longo tempo antes de se abrirem em t = 0 .

a) Em quantos microssegundos, depois da abertura das chaves, a energia dissipada no resistor de 4 k Ω é 10 % da energia inicial armazenada no indutor de 6   H ?

b) No tempo calculado em (a), qual percentagem da energia total armazenada no indutor foi dissipada?

Passo 1

Nesse caso, podemos criar um equivalente de Thévenin (Lembra deste assunto? Ele sempre é um quebra galho para circuitos lineares), para a esquerda do indutor e para a direita, um resistor equivalente.

Logo,

1 k Ω | | 4 k Ω = 0.8   k Ω

20 k Ω | | 80 k Ω = 16 k Ω

Para a fonte de tensão:

105 × 10 - 3 0.8 k Ω = 84   V

Logo, o circuito ficará da seguinte maneira:

i L 0 - = 84 16.8 = 5   m A

Passo 2

t > 0 - Nesse caso, o circuito ficará da seguinte forma:

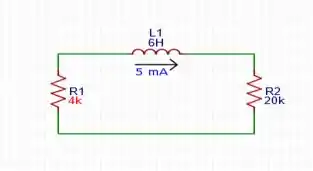
Para o cálculo da constante de tempo:

τ = L R = 6 24 × 10 - 3  

τ = 250 μ s ;   1 τ = 4000

Logo, a equação da corrente no indutor fica da seguinte forma:

i L = 5 e - 4000 t   m A ,     t ≥ 0

A potência no resistor de 4k:

p 4 k = 25 × 10 - 6 e - 8000 t 4000

p 4 k   = 0.10 e - 8000 t   W

E a energia armazenada:

w d i s s =   ∫ 0 t 0.10 e - 8000 x d x  

w d i s s = 12.5 × 10 - 6 1 - e - 8000 t   W

Para o instante t = 0, a energia é igual a:

w 0 = 1 2 6 25 × 10 - 6 = 75 μ J

Agora, o próximo passo é calcular os 10%:

0.10 w 0 = 7.5 μ J

12.5 1 - e - 8000 t = 7.5 → e 8000 t = 2.5

t = ( ln ⁡ 2.5 ) 8000 = 114.54   μ s

Assim, encontramos a quantidade que o resistor de 4k tem 10% da energia armazenada em relação ao indutor.

Passo 3

Agora, é calcular a energia dissipada total no indutor.

w d i s s t o t a l = 75 1 - e - 8000 t μ J

w d i s s 114.54 μ s = 45   μ J

% = 45 75 100 = 60 %

Assim, 60% da energia armazenada no indutor foi dissipada.

Resposta

a )   t = 114.54   μ s

b )   % d i s s i p a d a = 60 %

Exercícios de Livros Relacionados

Não há nenhuma energia armazenada no circuito da Figura P7.68 no instante em que a chave é fechada.Determine i 0 tp a r at ≥ 0 . Determine v 0 tp a r at ≥ 0 . Determine i 1 tp a r at ≥ 0 . Determine i
O centelhador do circuito visto da Figura P7.86 irá centelhar (ocorrerá nele um arco elétrico) sempre que a tensão em seus terminais alcançar 30 kV. A corrente inicial no indutor é igual a zero. O val
A corrente no indutor do circuito da Figura P7.85 é 25 mA, no instante em que a chave é aberta. O indutor será danificado sempre que a magnitude de sua corrente for igual ou superior a 5ª. Quanto temp
A forma de onda de tensão mostrada na Figura P7.82 (a) é aplicada ao circuito da Figura P7.82(b). A corrente inicial no indutor é igual a zero.Calcule v 0 ( t ) .Faça um gráfico de v 0 t em função de
A fonte de corrente no circuito da Figura P7.81 (a) gera o pulso de corrente mostrado na Figura P7.81(b). Não há nenhuma energia armazenada em t=0.Deduza as expressões numéricas de v 0 ( t ) para os i