Elabore um problema para ajudar outros estudantes a entender como obter a transformada de Fourier de uma determinada forma de onda usando a figura .
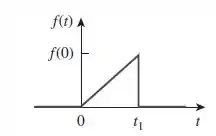
Passo 1
Galerinha, vamos resolver a seguinte questão: “qual é a transformada de Fourier do pulso triangular da figura?”.
Podemos expressar essa função da seguinte maneira:
Ou seja, temos um degrau unitário modelado pela função . Vamos aplicar a transformada de Fourier:
Resposta
A transformada é igual a: