Encontre o campo elétrico dentro de uma esfera com uma densidade de carga proporcional à distância da origem, , sendo uma constante. [Dica: esta densidade de carga não é uniforme e você deve integrar para chegar à carga encerrada.]
Passo 1
Falaaa, tudo belezaa?? Para acharmos o campo elétrico com a lei de Gauss usamos a fórmula abaixo:
Quer dizer que a integral do campo elétrico em uma superfície fechada é igual a carga envolvida dividida por uma constante. O que precisamos agora é definir a superfície e a carga envolvida. Bora lá!!!
Passo 2
O fio infinito e a superfície Gaussiana que vamos considerar estão abaixo:
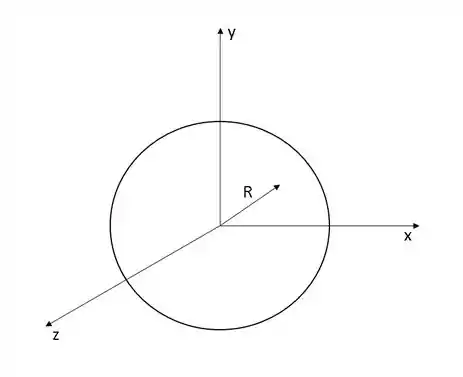
A superfície que vamos considerar podemos analisar que será a de uma esfera, sendo sua área de superfície definida por .
Porém, para a carga envolvida temos uma diferença dos exercícios anteriores. Neste exercício, a carga é proporcional a distância do centro, quer dizer que quanto mais perto da superfície da esfera mais carga. Portanto, temos que integrar essa carga.
Montando uma integral esférica para calcular a carga envolvida.
Substituindo os valores na fórmula do passo 1.