Encontre o campo elétrico a uma distância acima do centro de uma espira quadrada (lado ) que tem uma densidade de carga uniforme (Figura 2.8) [Dica: use o resultado do exemplo 2.1.]
Passo 1
Falaaa, tudo bemm?? Espero que sim!! Para resolvermos este exercício vamos usar o resultado do exemplo do livro assim como sugere o enunciado. O campo elétrico do exemplo 2.1 é:
Porém, vamos fazer algumas adaptações para se adequar ao exemplo. Bora lá!!!
Passo 2
A imagem que representa a espira e o ponto que estamos procurando o campo elétrico está abaixo:
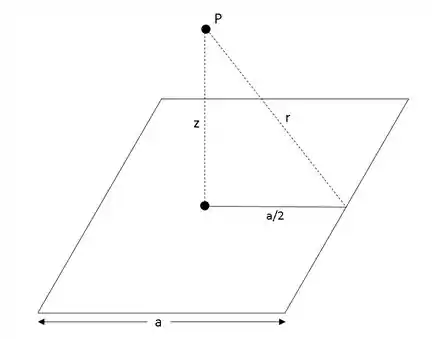
O que este exercício difere do exemplo do livro é que e . Substituindo no resultado do passo 1.
Como o ponto está bem no centro da espira. Então, o campo elétrico age apenas na componente vertical e temos 4 linhas.
E o cosseno de é o cateto adjacente sobre hipotenusa, sendo representado por:
Portanto, o campo elétrico do nosso exercício é: