Encontre o campo elétrico a uma distância acima de uma das extremidades de um segmento de linha reta (Figura 2.7) e que tem uma distribuição linear de carga uniforme, de densidade . Verifique se a sua fórmula é coerente com o que seria de se esperar para o caso de .
Passo 1
Falaaa, tudo bemm?? Espero que sim!! Para resolvermos este exercício vamos usar a fórmula do campo elétrico para carga uniforme abaixo:
Mas antes de substituirmos os valores precisamos interpretar a figura que o enunciado se refere. Bora para o exemplo!!
Passo 2
Antes de tudo, como o ponto em que estamos procurando o campo elétrico está em uma das extremidades da linha, nenhum vetor irá se cancelar. Então, teremos um campo no vetor vertical e horizontal.
Os parâmetros da fórmula podem ser analisados abaixo:
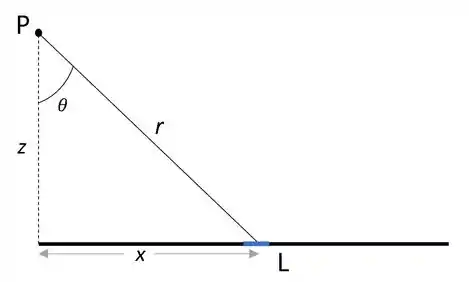
Estamos considerando uma parte infinitesimal da linha, representada pela cor azul.
Sabemos que o campo elétrico na componente vertical e horizontal são dadas por:
Vamos calcular um vetor por vez e depois o campo elétrico será a soma deles.
Como o enunciado nos diz que a densidade de carga é uniforme. Então, .
Enquanto que o cosseno de é cateto adjacente sobre hipotenusa.
Pela imagem, sabemos que o varia do ponto inicial até o fim da linha.
Pelo teorema de Pitágoras .
Resolvendo a integral por substituição trigonométrica, encontramos:
Agora, vamos encontrar o campo elétrico na horizontal. O campo elétrico que está sendo aplicado no ponto P é contrário a . Então, colocamos o negativo.
O seno é definido pelo cateto oposto sobre hipotenusa.
O continua com o mesmo valor da componente vertical e o também varia até o fim da linha.
Resolvendo a integral por substituição encontramos:
Aplicando os limites.
Portanto, o campo elétrico que queríamos encontrar é a soma dos que encontramos.
Portanto, caso o seja muito maior que o , o campo elétrico da componente horizontal irá se cancelar e a componente vertical se resumirá a: