Encontre o campo elétrico a uma distância do centro de uma superfície esférica de raio (Figura 2.11), que tem uma distribuição superficial de carga elétrica de densidade uniforme . Aborde o caso (interno), bem como (externo). Expresse suas respostas em termos da carga total na esfera. [Dica: use a lei dos cossenos para escrever em termos de e . Certifique-se de escolher a raiz quadrada positiva: se , mas é se .]
Passo 1
Falaaa, tudo belezaa?? Para a resolução desse problema vamos usar a formula do campo elétrico para densidade superficial abaixo:
Mas antes precisamos analisar a esfera e os parâmetros para definir os valores da fórmula. Bora lá!!!
Passo 2
Os parâmetros do exercício podem ser analisados na figura abaixo:
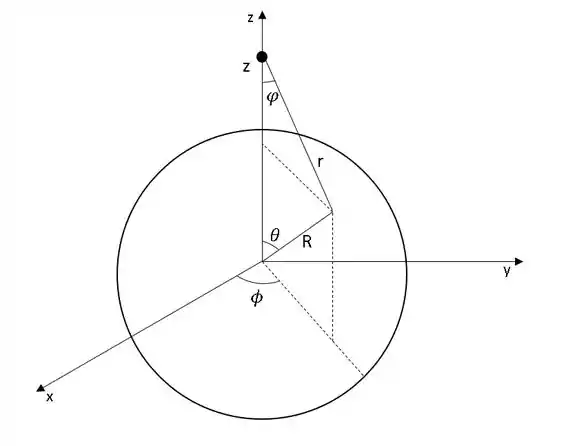
Pela imagem e com um pouco de análise geométrica podemos concluir:
Então, como o campo elétrico aponta na direção de , o campo elétrico é definido por:
O varia de até . Então, podemos colocar o resultado e remover as constantes.
Usando integração por substituição.
Ajustando os limites. Quando ; . Quando ; .
Sendo assim, quando , ou seja, o campo fora da esfera.
E dentro da esfera não haverá carga envolvida, então o campo será zero.
Resposta
Fora da esfera:
Dentro da esfera: