Encontre o campo magnético no ponto P no eixo de um solenoide enrolado de forma compacta (bobina helicoidal) com n voltas por unidade de comprimento, envolvendo um tubo cilíndrico de raio a e pelo qual passa a corrente I (Figura 5.25). Expresse sua resposta em termos de (é o jeito mais fácil). Considere que as voltas são essencialmente circulares e use o resultado do Exemplo 5.6. Qual é o campo no eixo de um solenoide infinito (infinito nos dois sentidos)?
Passo 1
Faaala, galerinha!! Como vocês estão? Partiu resolver mais uma questãozinha?
Para essa questão, adotaremos o seguinte desenho para nos orientarmos melhor:
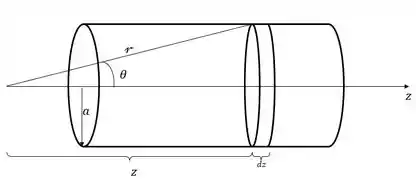
A partir da imagem acima, podemos determinar que o campo magnético presente é:
Porém, a partir da imagem vemos que Desse modo, temos que:
Desse modo, substituindo tais valores no campo já calculado, temos que:
Passo 2
Para um solenoide infinito, podemos afirmar que: .
Portanto,
Substituindo essa relação no valor do campo no eixo do solenoide, considerando os dois sentidos, temos que:
Prontinho, pessoal!! Bora resolver mais uma questão juntos?