(a) Encontre a força em um circuito quadrado posicionado como mostra a Figura 5.24(a), próximo a um fio reto infinito. Tanto pelo circuito como pelo fio passa uma corrente estacionária I.
(b) Encontre a força no circuito triangular da Figura 5.24(b).
Passo 1
Faaala, galerinha!! Como vocês estão? Partiu resolver mais uma questãozinha?
O circuito quadrado na figura 5.24(a) possui duas forças nos dois lados que se cancelarão. Isso se dá pelo seu formato quadrado.
Já na base, teremos um campo equivalente a:
A partir desse valor de campo estabelecido, podemos jogar na fórmula de força: .
Substituindo os valores, teremos:
No topo, teremos que um campo equivalente a:
Substituindo na mesma fórmula de força que usamos para calcular a força na base, teremos:
A partir das duas forças (base e topo), teremos uma força resultante equivalente a:
Passo 2
Já na imagem (b), adotaremos o seguinte esquema para sua resolução:
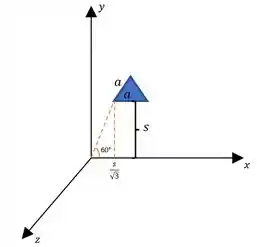
O campo na base será:
Portanto a força será:
No lado esquerdo do triângulo, o campo será em função de y e
Já a força aqui será calculada de uma maneira diferente, adotando como base, o esquema do plano cartesiano acima. Assim, utilizaremos:
Desenvolvendo a expressão acima, teremos:
Vemos que o componente z cancela o termo correspondente do lado direito, e que, portanto:
Aqui, temos que , portanto:
Além disso, observamos que a força do lado direito será a mesma. Portanto a força resultante no triângulo se dá por:
Prontinho, pessoal!! Bora resolver mais uma questão juntos?
Resposta
(a)
(b)