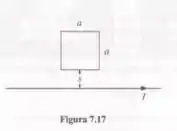
Uma espira quadrada de fio (de lado 𝑎) está em uma mesa a uma distância 𝑠 de um fio muito longo e reto, pelo qual passa uma corrente 𝐼, como mostra a Figura 7.17.
- Encontre o fluxo de B através da espira.
- Se alguém puxar a espira afastando-a do fio, a uma velocidade 𝑣, que será gerada? Em que sentido (horário ou anti-horário) flui a corrente?
- Se a espira for puxada para a direita à velocidade 𝑣, em vez de afastada?
Passo 1
Olá pessoal, bora para mais uma!?
Na letra A, queremos encontrar o fluxo magnético, sendo assim, temo que:
Para isso temos que encontrar o campo magnético devido a um fio muito longo, ou seja:
Substituindo B na expressão do fluxo magnético, temos que:
Passo 2
Agora na letra B, queremos encontrar fem, sendo assim temos que:
Como ds/dt=v, temos que:
Ou seja:
E com isso podemos perceber que a corrente flui no sentido anti-horário.
Passo 3
Na letra C, a espira será puxada para direita com uma velocidade v, sendo assim o fluxo magnético será constante, resultante então a .
Sendo assim, finalizamos mais uma! Até a próxima!