Uma espira quadrada, de lado a, está a meio caminho entre dois fios longos que estão no mesmo plano e a uma distância 3a um do outro. (Na realidade, os fios longos são os lados de uma grande espira retangular, mas os lados curtos estão tão distantes que podem ser desprezados.) Uma corrente no sentido horário I na espira quadrada aumenta gradualmente: (uma constante). Encontre a induzida na espira grande. Em que sentido a corrente induzida fluirá?
Passo 1
Olá pessoal, bora para mais uma!?
Primeiramente vamos fazer uma ilustração do que se trata neste problema, assim:
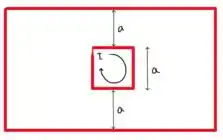
Assim, temos que:
Como é muito difícil calcular M usando uma corrente no pequeno loop, e como as bordas laterais são desprezíveis podemos encontrar o fluxo através do pequeno quadrado quando uma corrente flui no retângulo grande, ou seja,
Passo 2
Com essa associação, sabemos que o campo magnético devido a um fio longo é dado como:
Sabendo o campo, podemos usá-lo para encontrar o fluxo.
E o fluxo total será , devido a parte superior do retângulo e a parte inferior do retângulo, assim, temos que:
Assim podemos utilizar, para obter M, sendo assim, temos:
E agora temos que, ou seja:
Passo 3
Por último, temos que avaliar o sentido da calculada no item anterior. Se o fluxo líquido devido a corrente I no loop pequeno está na página e está aumentando, sendo assim a corrente induzida no loop grande é tal que o campo aponte para fora da página, sendo assim a é no sentido anti-horário.
Assim, finalizamos mais uma! Até a próxima.
Resposta
, anti-horário.