Uma espira quadrada (de lado a) é montada em uma haste vertical e gira à velocidade angular (Figura 7.18). Um campo magnético uniforme B aponta para a direita. Encontre para esse gerador de corrente alternada.
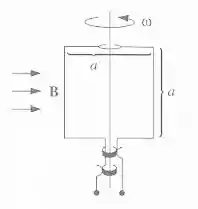
Figura 7.18
Passo 1
E aí galerinha, vamos explorar mais um probleminha de eletrodinâmica.
Neste problema, nosso objetivo é encontrar a , que é descrita como:
Então, se determinarmos o fluxo, só precisaremos derivá-lo em função do tempo para encontrar a .
Passo 2
O fluxo é descrito por:
Esse produto escalar pode ser descrito como:
Mas que será esse? Para identificá-lo, vamos olhar nosso sistema de cima.
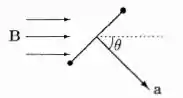
Onde o ângulo procurado, corresponde ao angulo entre a direção do campo e direção perpendicular a espira. A área será a parte mais simples de identificar, por como é uma espira quadrada de lado a, a área corresponderá:
Então podemos reescrever o fluxo como:
Mas, como podemos observar, o fluxo não apresenta uma dependência temporal, da forma como está escrito. Por conta disso, vamos ter que associar uma das suas variáveis com o tempo.
Passo 3
A alternativa mais óbvia é reescrever o como o produto do . essa notação já foi utilizada em outras ocasiões, como na descrição dos osciladores harmônicos. Então, agora podemos reescrever o fluxo em função do tempo, como:
Passo 4
Agora para encontrarmos a , precisamos derivar o fluxo em função do tempo:
E isso nos dá: