No Exemplo 3.8 determinamos o campo elétrico externo a um condutor esférico (raio ) colocado em um campo uniforme externo . Resolva agora o problema usando o método das imagens e verifique se sua resposta concorda com a Equação 3.76.
Passo 1
Falaa galera, bora iniciar mais uma questãozinha do nosso livro!
Bem galerinha, primeiramente para resolução do problema, iremos consultar a imagem abaixo. Cada carga real (em )tem uma carga de imagem em (). Deixe o eixo positivo estar na direção certa, então o ângulo é o ângulo esférico.
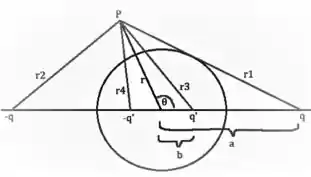
O potencial total é dado por:
, já que queremos e . Agora, o potencial é de aproximadamente, usando e :
Dessa forma, colocando mas mantendo constante, conseguimos replicar a solução da equação 3.76 do nosso livro!
E com isso a gente conclui nossa questãozinha, te vejo na próxima!