Uma haste de ferro de comprimento L e corte transversal quadrado (de lado a) recebe uma magnetização longitudinal uniforme M, e em seguida é dobrada na forma de um círculo na qual fica um pequeno vão (de largura ), como mostrado na Figura 6.14. Encontre o campo magnético no centro do vão, assumindo que . [Dica: trate como a superposição de um toroide completo mais uma espira quadrada com corrente inversa.
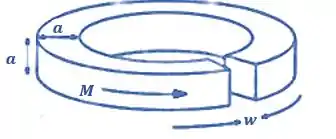
Figura 6.14
Passo 1
E aí galerinha, vamos explorar mais um probleminha de campos magnéticos na matéria.
Neste caso o enunciado já dá o caminho das pedras, quando nos fala para tratar o problema como a superposição de um toroide completo mais uma espira quadrada com corrente inversa.
Para um toroide completo, o campo dentro dele seria dado por:
Agora nosso problema maior será calcular o campo da espira quadrada.
Passo 2
O problema 5.8 já faz o cálculo que precisamos reproduzir aqui, então, basta pegarmos a equação geral do campo da espira quadrada e adequar ao nosso problema. Essa equação é expressa por:
Sendo a corrente estacionária neste caso, escrita por:
E o raio, será escrito em função de a, que é dado pelo problema. Logo, temos:
Inserindo nossas considerações na equação geral do problema 5.8, temos:
Se reorganizarmos a equação, teremos:
Passo 3
Agora, utilizando a dica, o campo no vão, pode ser expresso pela soma dos campos calculados acima, porém o campo da espera quadrada com a corrente inversa. Essa inversão implica na aparição de um sinal negativo no , assim teremos:
Podemos colocar em evidência.
Resposta
O campo magnético no centro do vão é expresso por: