Imagine que novas medições, extraordinariamente precisas, revelaram um erro na lei de Coulomb. Constatou-se que, de fato, a força de interação entre duas cargas pontuais é:
Onde é uma nova constante da natureza (tem dimensões de comprimento, obviamente, e é um número imenso – digamos, a metade do raio do universo conhecido – de forma que a correção é pequena, motivo pelo qual ninguém antes havia percebido a discrepância). Você está encarregado de reformular a eletrostática, de forma a acomodar a nova descoberta. Considere que o princípio da superposição continua verdadeiro.
a) Qual é o campo elétrico de uma distribuição de carga (substituindo a Equação 2.8)?
b) Esse campo elétrico admite um potencial escalar? Explique brevemente como chegou á sua conclusão. (Não é preciso prova formal - apenas um argumento convincente.)
c) Encontre o potencial de uma carga pontual – análoga à Equação 2.26. (Se a sua resposta para (b) foi ‘não’, é melhor voltar e mudá-la!) Use como ponto de referência.
d) Para uma carga pontual q na origem, mostre que
Onde é a superfície e o volume de qualquer esfera centrada em .
e) Mostre que este resultado pode ser generalizado:
Para distribuição de carga. (Esta é uma boa alternativa à lei de Gauss na nova ‘eletrostática’.)
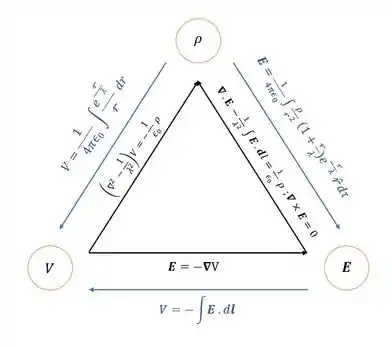
f) Desenhe o diagrama triangular (como na Figura 2.35) para este mundo, colocando nele todas as fórmulas apropriadas. (Pense na equação de Poisson como a fórmula para em termos de , e na lei de Gauss (forma diferencial) como uma equação para em termos de
Passo 1
a) Faaaala, galera! Bora fazer essa questão (um pouco diferente por sinal hahaha). Para dar a equação do campo elétrico substituindo a equação 2.8, que é dada por:
Basta aplicarmos a mesma correção feita na fórmula da força elétrica
Passo 2
b) Para provar se esse campo elétrico admite ou não um potencial escalar, devemos lembrar que o campo para uma carga pontual na origem é radial e simétrico, logo , o que também é valido para um conjunto de cargas (pelo princípio da superposição), ou seja, o campo admite SIM um potencial escalar.
Passo 3
c) O potencial elétrico é calculado a partir do campo elétrico, através da seguinte expressão:
Aplicando a expressão do campo elétrico encontrada anteriormente:
Podemos reescrever a integral da seguinte forma:
Resolvendo a integral, teremos:
Se integrarmos , teremos:
O segundo termo dessa integral, subtrai da segunda integral da equação , logo, teremos:
Portanto:
Passo 4
d) Neste item, o enunciado nos pede para mostrar que:
Para isso, vamos resolver uma integral por vez. Para a primeira integral, teremos:
Para a segunda integral, teremos:
Aplicando esses resultados na equação inicial:
Passo 5
e) Galera, aqui o enunciado nos pede para generalizar a expressão dada, o que quer dizer que a expressão deve ser valida para qualquer tipo de superfície gaussiana, seja ela esférica ou não esférica. Para provar que ela funciona, vamos fazer um relevo na esfera, empurrando uma seção circular para fora a uma distância do centro:
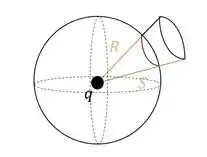
O elemento de área da superfície do relevo é dado por (quando está a uma distância do centro da esfera:
O elemento de área da superfície do relevo é dado por (quando está a uma distância do centro da esfera:
Agora, vamos calcular as diferenças para a esfera normal para a esfera com o relevo na aplicação dessa expressão:
Aqui podemos ver que a mudança na integral do potencial compensa a mudança na integral do campo elétrico , e com isso nós também chegaríamos ao resultado para o uso total da esfera com o relevo como chegamos na esfera convencional no item anterior. Podemos construir qualquer superfície fechada através de manipulações sucessivas de uma esfera, o que quer dizer que obteríamos o mesmo resultado para qualquer forma de superfície fechada. Além disso, pelo princípio da superposição se existirem muitas cargas na dentro da esfera a expressão será igual a . Como podemos ver no cálculo da esfera com o relevo cargas fora da esfera não apresentam contribuição no cálculo das integrais, ou seja, as integrais não sofreram mudanças por cauda de distorções na superfície esférica, desde que as cargas da distorção estejam no exterior da esfera. Portanto, essa expressão é válida para qualquer distribuição de cargas.
Passo 6
f) último item para finalizar, galera! Aqui o enunciado nos pede para desenhar um diagrama triangular (como o diagrama mostrado na Figura 2.35 do livro) utilizando as fórmulas apropriadas. Para isso, vamos primeiro escrever a forma diferencial para a “nova lei de Gauss” que encontramos, que ficará da seguinte forma:
Escrevendo toda expressão em termos de , ficaremos com:
E lembrando que , podemos montar escrever a equação de Poisson para as condições do problema:
E então, nosso diagrama triangular ficará da seguinte forma:
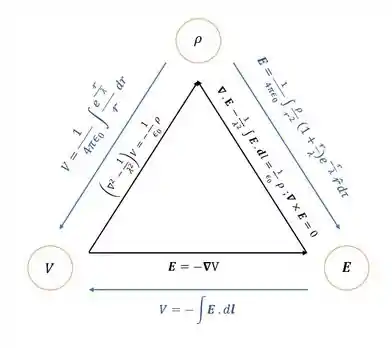
E aqui finalizamos a questão, pessoal! Até a próxima 😊
Resposta
a)
b)
c)
d)
e)
f)