Com a inclusão da força de reação de radiação (Equação 11.80), a segunda lei de Newton para uma partícula carregada torna-se
Onde é a força externa agindo sobre a partícula.
(a) Em contraste com o caso de uma partícula não carregada , a aceleração (como a posição e a velocidade) deve agora ser uma função contínua do tempo, mesmo que a força mude abruptamente. (Fisicamente, a reação de radiação amortece qualquer alteração rápida em .) Prove que é contínuo em qualquer tempo , integrando a equação de movimento acima de até e tomando o limite .
(b) Uma partícula está sujeita a uma força constante , que começa no tempo e dura até o tempo . Encontre a solução mais geral para a equação de movimento em cada um dos três períodos: .
(c) Imponha a condição de continuidade (a) em e . Mostre que você pode eliminar a divergência exponencial na região ou evitar a pré-aceleração na região , mas não ambas.
(d) Se resolver eliminar a divergência exponencial, qual é a aceleração como função temporal, em cada intervalo? E quanto à velocidade? (Este deve, é claro, ser contínua em e .) Assuma que a partícula estava originalmente em repouso; .
(e) Desenhe o gráfico de e , tanto para uma partícula sem carga quanto para uma partícula com carga (sem divergência exponencial) sujeitas a essa força.
Passo 1
Olá estudante!

Primeiro vamos analisar o que a questão quer.
Agora vamos utilizar as informações fornecidas por ela, vamos lá!
(a) Bom, temos que,
Onde é a força média durante o intervalo. Mas é contínuo, então, enquanto não é uma função delta, nós somos deixados (no limite ) com . Assim , também, é contínuo.
Passo 2
(b)
Onde é constante.
Onde é alguma outra constante.
Passo 3
(c) Em , ; Em , .
Então,
Para eliminar o fugitivo na região , precisaríamos de ; para evitar a pré-aceleração na região , precisaríamos de . Obviamente, não podemos fazer as duas coisas ao mesmo tempo.
Passo 4
(d) Se optarmos por eliminar o fugitivo, então
Onde é uma constante determinada pela condição
Onde é uma constante determinada pela continuidade de em :
é uma constante determinada pela continuidade de em :
Passo 5
(e)
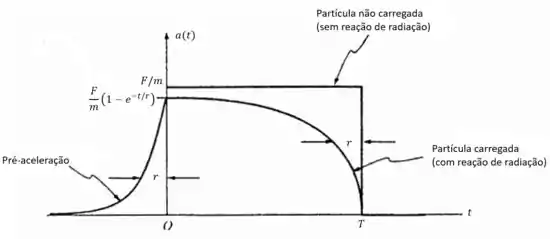
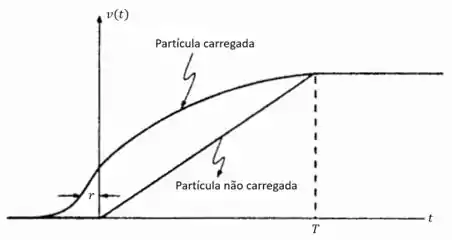
Resposta
Ver Passos 1, 2, 3, 4 e 5.