O índice de refração do diamante é 2,42. Construa um gráfico análogo ao da Figura 9.16 para a interface ar/diamante. (Assuma que .) Sobretudo, calcule (a) as amplitudes para incidência normal, (b) o ângulo de Brewster e (c) o ângulo ‘onde as curvas se cruzam’, no qual as amplitudes refletida e transmitida são iguais.
Passo 1
Faalaaa, tudo joia?? O enunciado nos pede para construirmos um gráfico que mostra a razão das amplitudes das ondas refletidas e transmitidas pela amplitude da incidente em função de . Onde, as equações são dadas por:
E o parâmetro para o alpha é dado por:
O gráfico pode ser analisado abaixo:
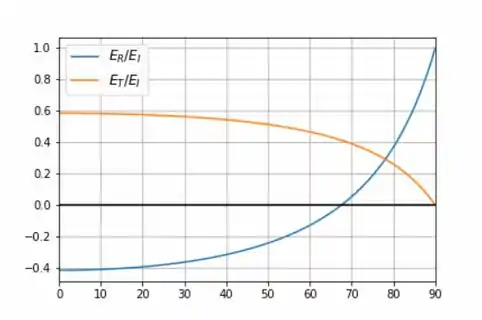
Passo 2
Na incidência normal , então :
Passo 3
No ângulo de Brewster . Logo, o ângulo de incidência é:
Passo 4
Quando a razão das duas amplitudes é igual, o ângulo também tem que ser igual:
Usando o alpha que definimos no Passo 1.