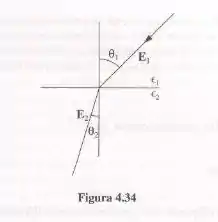
Na interface entre um dielétrico linear e outro, as linhas de campo elétrico se dobram (veja a Figura 4.34). Mostre que
Assumindo que não haja carga livre no contorno. [Comentário: a Equação 4.68 lembra a Lei de Snell na ótica. Uma ‘lente’ convexa de material dielétrico teria a tendência de ‘focar’ ou ‘desfocar’ o campo elétrico?]
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Seja a direção x tangencial ao plano e a direção y perpendicular ao plano. Além disso, deixe que as linhas de campo estejam apenas no plano xy. Então,
Logo, temos que
Dividindo a equação da esquerda pela da direita
Simplificando, nós temos que
Uma lente necessariamente tem que ter , assumindo (ar), portanto, , com isso, haverá um ‘desfoque’ do campo elétrico.
Resposta
Respondido acima!