Uma linha de carga uniforme é colocada em um fio reto infinito, a uma distância acima de um plano condutor aterrado. (Digamos que o fio corre paralelo ao eixo e diretamente acima dele e que o plano condutor é o plano .)
a) Encontre o potencial na região acima do plano. [Dica: refira-se ao Problema 2.47.]
b) Encontre a densidade de carga induzida no plano condutor.
Passo 1
a) Faaala, galera! Bora pra mais uma. O esquema para o problema é o seguinte:
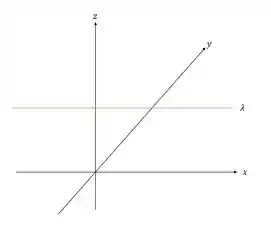
Como o enunciado nos sugere, utilizaremos o problema 2.47 como referência, portanto o potencial será calculado de seguinte forma:
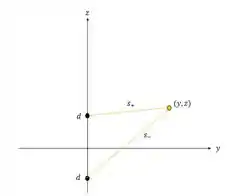
Passo 2
b) Para a densidade de carga induzida no condutor, utilizaremos a seguinte expressão:
No nosso caso , em . Com isso aplicando a derivada parcial em e utilizando a expressão acima, teremos:
Portanto:
E aqui finalizamos a questão, galera! Até a próxima 😊