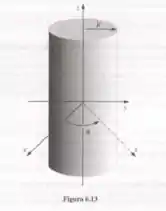
Um longo cilindro circular de raio R tem magnetização , onde k é uma constante, s é a distância a partir do eixo e é o vetor unitário azimutal usual(Figura 6.13). Encontre o campo magnético devido a M, para pontos internos e externos ao cilindro.
Passo 1
Olá pessoal, bora para mais uma!?
Primeiramente sabemos que:
Agora, temos que:
Com isso podemos perceber que a corrente flui pelo cilindro e retorna pela superfície.
Passo 2
Como estas duas correntes calculadas no passo 1 tem simetria cilíndrica, podemos obter o campo pela lei de Ampére.
Observe que , assim temos que:
Ressaltando que o resultado acima é para dentro do cilindro, para fora do cilindro resultando também em B=0.
Assim finalizamos mais uma questão, estou te aguardando na próxima!
Resposta
, dentro.
B=0, Fora.