Mostrei que no máximo um ponto da trajetória se comunica com em qualquer tempo dado. Em alguns casos, esse ponto pode não existir (um observador em não veria a partícula – na colorida linguagem da Relatividade Geral, ela está ‘além do horizonte’). Como exemplo, considere uma partícula em movimento hiperbólico ao longo do eixo x:
(Na relatividade Especial, essa é a trajetória de uma partícula sujeita a uma força constante .) Desenhe o gráfico de versus . Com quatro ou cinco pontos representativos na curva, desenhe a trajetória de um sinal de luz emitido pela partícula naquele ponto – tanto no sentido de x positivo quanto no de x negativo. Que região do seu gráfico corresponde aos pontos e tempos dos quais a partícula não pode ser vista? Em que tempo alguém no ponto vê primeiro a partícula? (Antes disso o potencial em é, evidentemente, zero.) Depois de já ter sido vista, uma partícula pode desaparecer do campo de visão?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
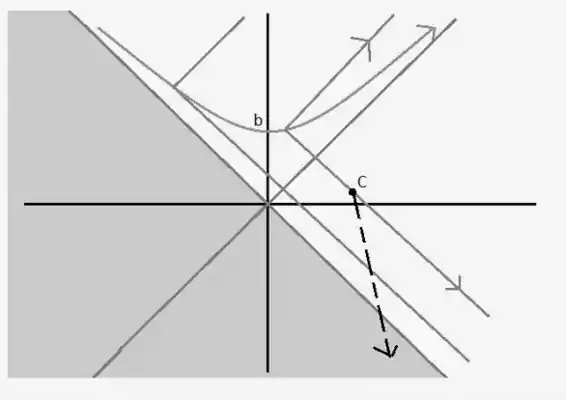
Defina a escala do sistema de coordenadas para que o caminho de uma partícula de luz seja uma linha com inclinação de 1. Em seguida, as duas linhas vermelhas representam os fótons emitidos no início (partícula começou a ir em direção à origem) e final (luz emitida quando as partículas estão de volta ao infinito).
Linhas cinzas representam fótons disparados em dois pontos que escolhi aleatoriamente. A linha azul é o caminho da partícula.
É óbvio que qualquer observador na área cinzenta não verá a partícula, pois a luz ainda não o atingiu. Se ele vir a luz (digamos que ele esteja em C), então para não a ver (a partícula) ele precisaria se mover para a área cinzenta, mas então o valor absoluto de sua velocidade seria maior que a velocidade da luz, já que o a inclinação de sua trajetória seria maior que 1. Assim, uma vez vista, a partícula estaria sempre à vista.
Além disso, mesmo que ele esteja na área cinza, já que ele não pode se mover mais rápido que a luz, a luz acabará por alcançá-lo.
Resposta
Respondido acima!