Paul DeYoung, do Hope College, assinala que como os cilindros do Exemplo 8.4 são deixados em rotação (em velocidades angulares, digamos, e ), existe na realidade um campo magnético residual e, portanto, momento angular nos campos, mesmo depois que a corrente no solenoide foi extinta. Se os cilindros forem pesados, essa correção será desprezível, mas é interessante resolver o problema sem esse pressuposto.
(a) Calcule (em termos de e ) o momento angular final nos campos. (Defina , então e poderiam ser positivos ou negativos.)
(b) Como os cilindros começam a girar, seus campos magnéticos variáveis induzem um campo elétrico azimutal extra que, por sua vez, dá uma contribuição adicional aos torques. Encontre o momento angular extra resultante e compare-o com seu resultado para (a).
Passo 1
Falaaa, meu querido/minha querida!!! Para resolvermos este exercício, vamos precisar usar os parâmetros da figura abaixo:
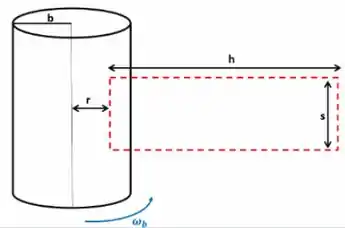
Vamos para a resolução que irei definir cada equação conforme a solução. Bora láa!!!
Passo 2
Usando a lei de Ampere para determinar o campo magnético dentro do cilindro maior, e a espira que escolhemos é uma retangular, como pode ver na imagem acima:
A corrente envolvida será devido às cargas na superfície que se movem com velocidade angular
Onde, . Logo, a lei de Ampere se torna:
O que definimos acima, é o campo magnético devido ao cilindro externo, em qualquer ponto dentro dele. .
Pelo mesmo método, o campo produzido pelo cilindro interno dentro dele é:
Onde, .
Sendo o campo total, então:
Agora, para o campo elétrico, aplicando lei de Gauss descobrimos que só existe campo elétrico entre os dois cilindros e ele é dado por:
Portanto, a densidade de momento é:
Calculando a densidade de momento angular:
Com isso, o momento angular total é a multiplicação da densidade de momento angular pelo volume total entre os dois cilindros:
Passo 3
O campo elétrico extra induzido pela mudança do campo magnético é dado por:
Enquanto que o fluxo, é dado pela soma do fluxo do cilindro interno e da casca cilíndrica. Sendo definido por:
Substituindo o valor do fluxo no campo elétrico:
Então, no cilindro interno:
No outro cilindro:
Calculando o momento angular em cada cilindro:
Por fim, o momento angular extra total é:
Encontramos o mesmo resultado a letra (a), porém com sinal oposto!!