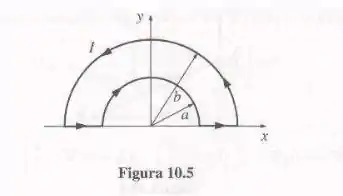
Por um pedaço de fio dobrado na forma de espira, como mostra a Figura 10.5, passa uma corrente que aumenta linearmente com o tempo:
Calcule o potencial vetorial retardado A no centro. Encontre o campo elétrico no centro. Por que esse fio (neutro) produz um campo elétrico? (Por que você não pode determinar o campo magnético a partir desta expressão para A?)
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, usaremos a letra como a distância da fonte ao ponto de interesse. O potencial magnético é dado por esta expressão
Onde essas integrais pertencem a pedaços de fio (1,2,3,4) como na imagem. Vamos fazer a integral primeiro
Apenas a componente do campo potencial vetorial na direção das peças 2 e 4 (chame-a de direção x) sobreviverá à integração, então:
Essa integral nos dá o seguinte resultado
A integral tem exatamente a mesma forma, mas de e integramos na direção oposta, então:
As duas estão na direção x.
Passo 2
Agora, nós vamos calcular as integrais e :
Desenvolvendo um pouco mais, nós temos que
E para a integral :
Passo 3
Portanto, o potencial do vetor magnético total está na direção x e é igual a:
Que nos fornece o seguinte resultado
O campo elétrico é então: